接上期的坑,这一期重点聊聊伯克利大学的BLEEX外骨骼采用的灵敏度放大控制策略。强烈建议没有看过上一期的去上一期补补,不然这一期十分可能云里雾里。
上期传送门:
打荷雨:以BLEEX为例,谈谈外骨骼的技术原理132 赞同 · 22 评论文章
本期将会有大量的控制学方面的内容,如果对外骨骼的控制此不感兴趣,呃,那还是去看科幻电影去吧。(因为控制策略是现实外骨骼技术很重要的组成部分啊)
引子
首先,先请大家想一想,怎么去控制一个机械臂到达你想要的位置(前提是这个位置在机械臂的可达范围内)。
有过相关机器人科创经验的想必已经有了思路。
比如,对于一个单个旋转关节的机械臂,旋转点固定,那么问题就变成了——怎么控制机械臂绕旋转点摆动到你想要的角度。
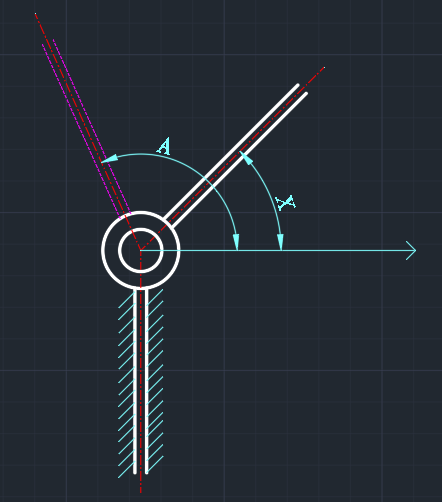
你说,采用位置控制。测量机械臂目前的角度,然后计算距目标角度的差值 ,差值有正负。
如果e是正的,那么说明机械臂目前的位置落后于目标位置,需要驱动机械臂往角度增大的方向运动。如果 是负的,那么驱动方向相反。
可以设定驱动机械臂的速度由差值 的绝对大小决定,如果
很大,那么速度就很快,如果
很小,靠拢速度也就很小。理想状况下,当差值
为0时,这个机械臂被驱动的速度也为0,那么就成功地控制机械臂到我想要的位置了。

不错,控制学门派第一招——P控制(比例控制),你已经掌握了。比例控制的核心思想就算将误差量成比例地通过执行机构施加于被控制对象上,所谓“敌进我退,敌退我进”。
但是比例控制,容易想到的是,被控制对象容易在目标位置处振荡,总是到达不了目标点,因为一不小心越过了目标点就要受到反向控制返回去,这个振荡造成了稳态误差。
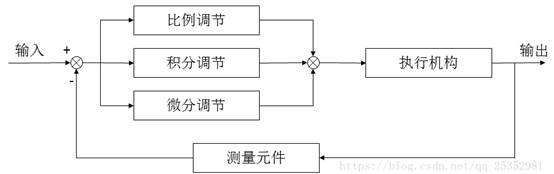
为了提升控制效果,消除P控制的稳态误差,以及改善P控制的动态性能,你还需要学习其他两招——I控制,D控制。这三招,合起来就是称霸广泛控制领域的PID控制(比例、积分、微分控制)!网上已经有讲的很详细的PID控制算法的文章了,这里不细讲其细节。
位置控制的前提是,你需要提前已知机械臂要到达的理想位置,也就是说,你需要提前知道机械臂运动的理想轨迹。但是这个问题在外骨骼机器人上,由于目标任务是让外骨骼跟随人体运动,而人体想怎么动很难量化。
你想一下自己,当你想要向前走的时候,你会清楚地知道自己大腿要转动多少度、小腿要绕大腿转多少度、落脚点在哪儿吗?很难,因为走路这一详细动作过程已经通过从小的学习,被控制身体运动的脑干控制着。而想弄清楚大脑怎么想,以目前的脑科学仍然是很难。

那么是没有办法了吗,当然不是,只不过这给现今的机器人研究带来了新的挑战。以前的机器人控制研究,是不需要考虑与一个有智慧的柔体动物打交道的。工业机器人最初的用途也无非拿起一些零件,将其准确地送到或安装到某个位置;又或是无人小车这种机器人,又不需要与被搬运的物品进行交互,最多知道自己运送的是什么物品,有什么属性,应该送到哪里这类规划问题。
要与人交互,还要达到和人体跳探戈这种“柔顺”的地步?对不起,除了宅男的幻想,很长一段时间内没有这个需求。

随着柔性制造概念的发展,工业4.0、中国制造2025等计划的提出,在未来需要让工厂智能化,这就对制造的柔性提出了需求,也就是为了个性化的制造任务,能迅速整合制造资源进行多元加工的能力。那么在柔性制造里,机器人的柔性也开始得到关注。
比如,一台负责安装轴类零件的机械臂,需要将轴零件装入孔类零件。那么如果机械臂位置没对准,轴偏了一点,那么这点角度误差会让系统不停地去修正,那么会在机械臂关节持续地造成大的驱动力矩,而柔性会减小这个关节驱动力矩,不至于力矩过大弄坏零件甚至机器人本身。

形象比喻就是,你搬一个轴去装到孔里,你搬不动轴,轴歪了一点,那么硬怼它是怼不进去的,你使再大力气也没用。你得蹭一蹭,轻轻拨动一下轴的角度,也许轴就被蹭进去了。能完成蹭一蹭这个动作就需要你有一定的柔性。
这个对工业机器人的柔性要求,和外骨骼要求和人体柔顺跟随的要求,好像很相似啊!

因此,近些年来,机器人的柔顺控制方法陆续的被提出来,如阻抗控制(将机械臂末端与环境看成通过阻抗模型连接)等方法,也逐渐从工业界应用到了外骨骼控制研究上。但这些柔顺控制方法不是本期讨论的重点。
但是,工业机器人要求的柔性,是在已知参考轨迹的前提下,通过力控制让机器人柔顺地安照参考轨迹来运动,在运动期间可以感知环境的作用,从而能够进行避让。这些柔性控制是基于能获得参考轨迹而达到的柔性。
那么话说回来,由上所述,我们很难知道人想怎么运动,也很难获得外骨骼想要的参考轨迹输入量,那该如何让外骨骼跟随人体呢?换句话说,没了参考轨迹,该怎么解决跟随问题呢?
我们接下来要讨论的BLEEX的灵敏度放大法解决了这个问题。而它的控制思路却是,不提供参考轨迹输入量。
接下来的内容会涉及到自动控制原理的一些基础知识,还有高中水平的数学推导,如果实在不想看数学的同学可以直接去看结论。
(不过我已经尽我所能去讲的很通俗了,真的不看嘛?)
先来看看一个开环控制模型
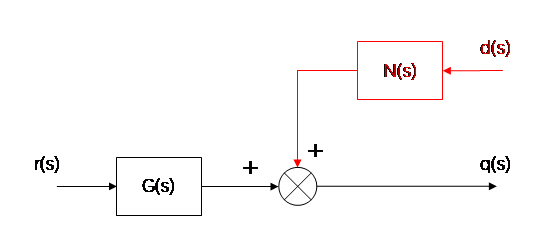
控制模型框图中,一个控制量经过一个方框,代表这个量乘以方框代表的函数。而这个打叉的圆代表一个结点,结点的输出等于结点输入量的代数和,结点的输入量可以被加进结点,也可以被减进结点。上述控制模型没有从输出得到反馈,整个控制线路看起来像一条链而不是一个环,所以叫开环控制。
这种开环模型的含义是,输入控制量r是我们想要达到的理想量,经过系统的模型函数 后得到一个用于控制的量,这个量的量纲与输出控制量
是一样的。
比如我想让机械臂运动到某一角度,这个理想量 是角度,但是我用来控制机械臂的控制量
却是驱动模块的电压值。而这个系统模型函数
就是将角度通过机械臂的运动学、动力学模型转换成相关的电压值的函数。
同时,在实际环境中总是存在各种扰动,如机械阻尼、摩擦、空气流动、天气不好、心情不好等,这往往让实际被控制对象到达不了我想要的理想量,因此系统的实际输出包含了我们主动控制的部分和环境扰动的部分。
因此上述开环控制系统得到的输出表达式为:
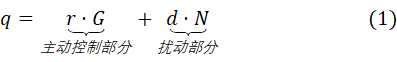
这里针对闭环系统的传递函数求解方法做一个简单预习(对于学过自动控制原理的同学应该叫复习)
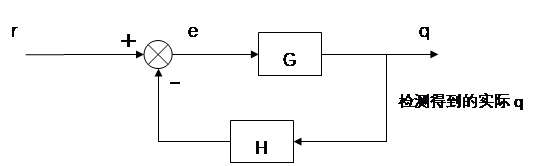
可以列出一个方程组:
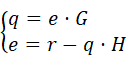
消去 ,得输出量
的表达式为:

在已知系统模型 和反馈函数
的情况下,闭环系统输出量
可以表达为输入量
的关系式。
其中 称为该系统的传递函数。
可以看出,此闭环系统的反馈回路最终会与理想输入量 作差,得到误差量
。那么达到的效果就是,当这个误差值
,即理想量
大于输出量
,那么说明控制系统还需要努力,加把油,因此会将正值
输入到系统模型
中,得出一个正的控制量
,并在下一周期加到控制对象上去。如果
,则整个过程相反。由此可见,该系统是一个带有负反馈调节功能的系统。
而如果将反馈回路得到的值与理想输入量 作和,会怎么样呢?改写的控制框图如下所示:
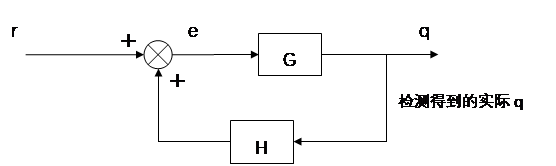
同样列出方程组:
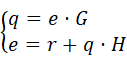
同样消去 ,得输出量
的表达式为:

我们发现,当我们把作差改为作和,传递函数的分母也由 变成了
。
那么改过之后有什么变化呢?当 和
都是单调增加函数时(如正比例函数),我们发现,随便输入一个正的控制量
,在经过输出和反馈相加后,得到的
依然是正的,且下一轮的
比这一轮的
还要大。照此循环下去,这个
将会逐渐增大最后变为无限大,最后输出的控制量
也会是无限大。这是一个正反馈系统!
由上可见,传递函数形式如 或
的,都能看出是一个闭环系统,根据分母是加还是减可以看出这个系统是负反馈系统还是正反馈系统。
预/复习完毕!
接下来,我们将图1的开环系统升级成闭环控制系统,将输出量作为反馈,并与理想输入量作差,然后将这个误差值 作为系统模型
的输入。又考虑到输出量
和输入量
不是一个量纲,因此在反馈回路上要串联一个反馈函数
。这个闭环系统如下所示。

这个系统因为输出量 返回了反馈量,形成了一个环,因此叫闭环系统。下面,我们来求一下这个系统的输出表达式。
由于扰动 和输入量
都可以看作是对系统的输入,因此系统输出可以通过这两者单独输入的线性叠加得到。
当扰动 为0,
作为输入量时,系统框图简化为下图。
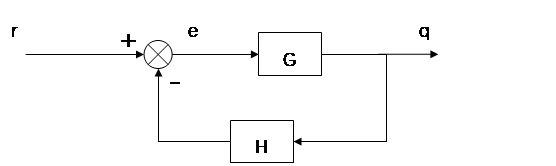
可得输出量 为输入量
的表达式:
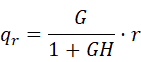
当输入量 为0,
作为输入量时,系统框图简化为下图。
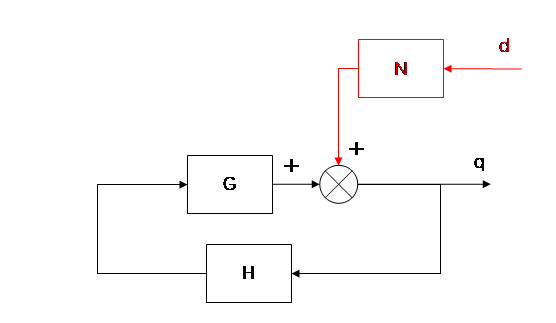
此时将 和
作为反馈回路上的函数,可直接列出:
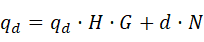
即可得输出量 为扰动量
的表达式:
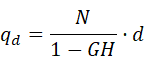
综上,将输入量 和扰动量
各自得出的输出量
,
线性叠加,即得到输出量q的表达式:

从这个表达式可以看出,在有扰动存在的闭环控制系统(图4)中,系统的输出为主动控制部分和扰动部分之和。其中主动控制的部分为负反馈闭环,扰动部分为正反馈闭环。
通常,扰动部分都为正反馈,这在日常生活中广泛体现。比如,你精心策划的一场活动因为一场飘忽不定的天气而完全失败;你认真计算了很久的习题因为一点点疏忽大意而全部算错;一个小小的病毒因为一场罕见的食野味的憨憨行为而迅速传播,突然就引起了全国性的疫情。

在自然面前,可控是少见的,不可控才是常见的,一点小小的扰动就能要你命3000,更何况是对于设计的不好的控制系统,任何未知的扰动都有可能带来灾难性的后果。
因此,长期以来人们对控制系统的研究,都是为了消除扰动带来的灾难性影响。人们认为扰动对控制系统是非常有害的,是必须强烈遏制的,许多控制方法都有效地将扰动对系统带来的影响大大降低,从而获得一个健硕的(Robust(也称鲁棒的))系统。
那些不稳定的东西,会让我们更强——尼采
BLEEX的研发人员们,在“扰动”这个通俗意义上的危害中看到了希望,因此,他们发出了以上感叹。

我们换一个思路,将外骨骼本身看做一个系统,将人看做环境。上面不是说了么,我们很难知道人体想要怎么运动,因此我干脆不去检测你怎么运动了,我就把你看做一个扰动。
由上期讲到,BLEEX的传感器系统里,用来输出力的液压缸末端装有一维力力传感器,而穿戴者和外骨骼之间没有什么交互力的传感器(除了足底压力传感器,那是用来检测负载分布在哪只脚上的)。因此,伯克利大学BLEEX团队采取了只检测外骨骼受到外界施加给自己的力或力矩的方案。人的腿相对外骨骼腿杆有位置误差,那么人的腿会给外骨骼带来交互力,这个力通过外骨骼自身机械结构的传导,传递到了液压缸作动器末端的力传感器上。
虽然没有人机直接的交互力传感器,但是BLEEX依然间接地测到了人体对外骨骼的影响。那么理论上说,不仅是人,外骨骼系统以外的所有环境都会对其造成影响。这一部分的讨论将在后面进行。
因此,我们将图4的输入量 抹去(反正也没办法得到),我们得到一个图5的系统。
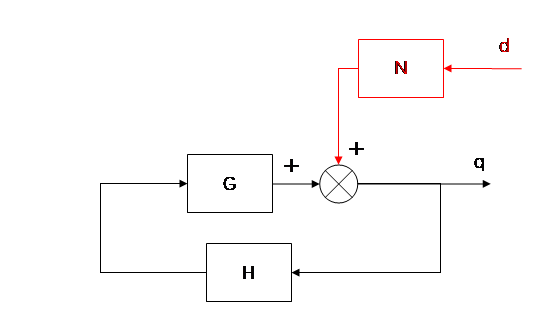
然后,我们把这个图里的框框挪一下位置。为了和原文献字母使用一致,方便大家看文献,将扰动函数 的字母换成
,将反馈函数
字母换成
(Controller)。
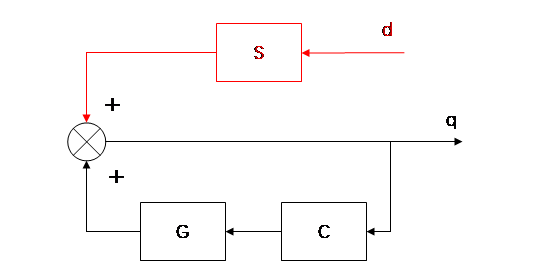
在图8里,当以BLEEX外骨骼作为对象来讲时,那么各个框图的含义将改为:
为穿戴者对外骨骼造成的关节力或力矩,经过传递函数
的映射,其量纲与各关节的运动学量(角度、角速度、角加速度)
分别相同。
各关节的运动学量 会通过大小腿杆的加速度计、关节编码器等方式反馈,经过控制器
和系统的运动学和动力学模型函数
,又变成了下一轮的控制量。
现在来求解外骨骼运动学量 的表达式,由图8可得:
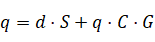
继续合并 得:

一眼看出,该系统为正反馈闭环系统!
其实,这个系统和图6的系统没有区别。正如之前所说,将人的对外骨骼的操作当作环境扰动,那么图8和图6一致,没问题。
那么,接下来就是灵敏度放大法的核心了(怎么这么久才到重点)
灵敏度放大控制器
- 首先,我们知道该系统有一个闭环,这个闭环是经过了外骨骼的模型
,因此该闭环属于外骨骼机器人系统内部的控制闭环(有点绕,将穿戴者看作外界来理解),且这个环里有一个控制器
。
- 其次,我们知道了系统的输出量
(运动学意义上的,关节角度、角速度、角加速度),是可以通过穿戴者对外骨骼施加的力矩
来表达。
- 然后,我们观察到该系统的传递函数为正反馈传递函数。

懂了灵敏度放大的意思了吗?
似懂非懂?
那我再解释一遍。
人 对 外骨骼 的影响 通过正反馈闭环传递函数 输出了很高的
。
上面提到了控制器 ,为什么要将反馈函数
理解成控制器?因为它可以由我们定义其具体表达式,它是可设计的。
如果设计这个控制器 ,能够让人对外骨骼的控制,线性地放大。每一点小小的
的增加,会带来大大的输出量
的增加,即
曲线的斜率很大,这就是灵敏度很大的意思。
外骨骼的运动学及动力学模型都由机械结构决定了,因此这个外骨骼模型 一般是不能变动的。所以这个控制器
,就是实现灵敏度从很小放到很大的关键。
先为了消除传递函数分母的 ,将
设计为
,但是这会导致分母为0。
因此加上一个比例系数 ,将
设计为
,分母就变成
,如果
,那么
,
前面的系数是大于1 的,因此灵敏度被放大了。但是这样做看起来太不方便了。
因此将控制器设计为:

那么式(5)就可以表示为:

这个 就定义成灵敏度放大系数,这个控制器
就为灵敏度放大控制器。
回到我们最开始所讲的那个开环控制模型(图1),其输出量 的表达式(1)为:
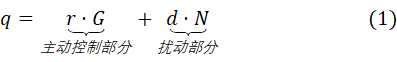
一对比,我们发现:式(6)将主动控制部分舍弃,且将扰动部分通过灵敏度放大系数 放大。其意义是:将人体看做环境扰动后,让外骨骼对环境扰动更加灵敏,也就实现了人体对外骨骼操纵的灵敏。如果灵敏度放大系数
为10,那么就意味着相比式(1)的控制系统,式(6)的控制系统将扰动部分的灵敏度放大了10倍,以前作用到外骨骼上一个单位的力输出了
的输出量,现在将会输出
的输出量。
灵敏度放大法,搞定?
其实从构建来说,灵敏度放大法的构建任务已经搞定。
但是仍有许多问题需要思考。
问题1:为什么一定要是正反馈?负反馈不行吗?
答:
如果你将图8的控制框图里下方的反馈回路的 号改成
号。那么传递函数就会变成:
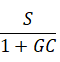
这是个负反馈的传递函数没错,但是你为了获得线性的灵敏度放大表达式 ,你需要将控制器重新设计为:
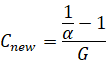
等等,这不和没改之前的控制器 差个负号吗?
。
没错,尽管你将反馈回路改成负反馈,但是控制器为了获得同样的表达式又会生成一个新负号,这个负号又会将反馈回路改回正反馈。
其实这个正反馈是我们从图6里的扰动闭环得来的,与其说是我们设计成正反馈,不如说正反馈本来就是扰动闭环系统的特性。
问题2:既然是正反馈,你怎么知道这个方法是稳定的?
答:
这个问题超纲了,对于控制系统的稳定性分析需要较高水平的控制学理论基础,这个还得等我回去学习学习。目前一个通俗的解释就是,既然人在系统里扮演了扰动的角色,那么外骨骼一定会响应这个扰动,因此作为智慧生命的穿戴者,他不会允许这个系统失控。
就算包含了控制器 的外骨骼闭环是正反馈,但是包含了传递函数
的人机反馈闭环可以稳定整个人机系统。(不要打我,这是BLEEX论文里[1]的原话,这个传递函数
在后面会提及)
问题3:灵敏度放大法对使用环境有什么要求?
答:
灵敏度放大器 的表达式中有系统模型
:

因此必须要精确得知道系统模型 ,否则就会引起输出误差。
下面,我们对系统内的模型存在误差,引起输出量 的变动做一个分析。
——————————————
(以下分析需要具备高等数学知识)
首先,研究对象是模型误差造成的 的变动,因此要假设人体输入量
不变。
然后,系统模型 是需要通过对外骨骼的运动学、动力学进行建模的,建模精度肯定和实际有一定的误差,因此
是个变量,其变动量为
。
扰动函数 将穿戴者对外骨骼造成的力矩
转化成与外骨骼运动学输出量
相同量纲的控制量,因此也需要建立一个关于扰动力矩到运动参数的控制模型,所以扰动函数
同样存在误差,其变动量为
。
而灵敏度放大器 是自行设计的一个功能传递函数,因此不存在误差,为常量。
综上,系统模型 与扰动函数
作为变量,输出量为
,即
为
与
的二元函数,即
。为了求得
的变动量
,对
做全微分:

我们知道, ,因此
和
分别计算得:
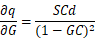
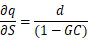
因此, 的全微分为:

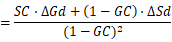
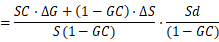
注意到 就是
,因此:
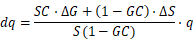
可以获得输出量全微分 与原输出量
的比值:
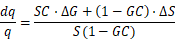


在离散系统中,输出量的全微分 其实就是其变动量
,因此,我们获得了输出变动量
与系统模型变动量
和扰动函数变动量
的关系:

我们假设我们构建的扰动函数是没有模型误差的,即 。而外骨骼的系统模型
因为建模不精确等原因,有10%的误差,即系统模型变动量
占理想系统模型
的10%。代入式(7)来看看系统输出的变动量
为多少:
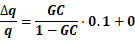
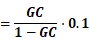
灵敏度放大器 ,取灵敏度放大倍数
为10,即
,即:
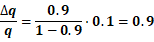
即当系统模型精度仅有10%的误差时,输出量的变动量 将会占到理想输出量
的90%!如果变动量为增量的话,几乎就是翻倍输出!超级加倍,怕不怕?
分析完毕。
——————————————
因此使用灵敏度放大法的最大要求就是,你建立的系统模型一定要足够精确,不然输出也将“更加灵敏地放大”。因此BLEEX的团队在讲其控制方法的论文里,前半部分讲灵敏度放大法,后半部分就全是在讲建立外骨骼的动力学模型了。
问题4:怎么区分穿戴者对外骨骼造成的扰动,和其他事物对外骨骼造成的扰动?
答:
区分不了。对,就是区分不了。
BLEEX的团队解释道,如果有人推了外骨骼一把,外骨骼是会响应这个推的动作的,就像一根芦苇一样,能被任何风吹草动所惊扰。那么,穿戴者穿上了外骨骼,因为被推了,身体不平衡,那他肯定要去控制自己的身体保持平衡。那么外骨骼此时会因为穿戴者保持平衡的动作也平衡下来,从而人机系统因为人的挣扎相安无事。

但是这样做,需要外骨骼能很快响应人体下意识瞬间做出的动作,因此要求外骨骼有很高的控制带宽(能够响应更高频率的控制信号,它的控制频带就更宽了),还要要求穿戴者有敏捷的身手。
同时这也会引来一个新的问题——怎么区分负载?
问题5:如果负载也算作环境扰动的话,那么背上34kg的重物,重物本身也会对外骨骼产生扰动啊。如果要让人去对负载产生的扰动时刻不停的“挣扎”,那人不就相当于自己背上负重了么?
答:
BLEEX的团队没有问出这个问题,我想应该是在实验中穿戴者的确感觉不到负载的重量,也就不会问出这种问题。
我对这个问题的理解是,因为灵敏度放大器 将外骨骼的灵敏度放大了。一种普通的控制系统,它对扰动是克制的,因此如果我去干扰被控对象,被控对象会在控制作用下“顽固不动”。就拿开头引子里举过的机械臂的例子:
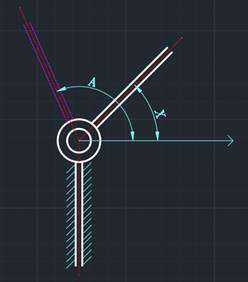
如果采用普通控制,当机械臂到达 位置时,我应该是很难掰动机械臂的,就算掰动了,它也会在控制下逐渐重新回到
位置,这算一种控制稳定。
当我在这个机械臂模型上使用灵敏度放大控制后,我作为扰动,可以很轻松得移动这个机械臂。怎么想象这种感觉呢,就像这个机械臂没有装驱动关节电机一样,推它的感觉就像是推一个没有动力的连杆一样,但是我去推它而不抓住它的话,它又会在正反馈下越转越快。
然后,我需要用这个灵敏度放大机械臂去帮我完成我自己不能完成的任务,比如把一个重物从 位置搬到
位置。那么相当于在其末端绑上一个重物
,我去推这个机械臂。
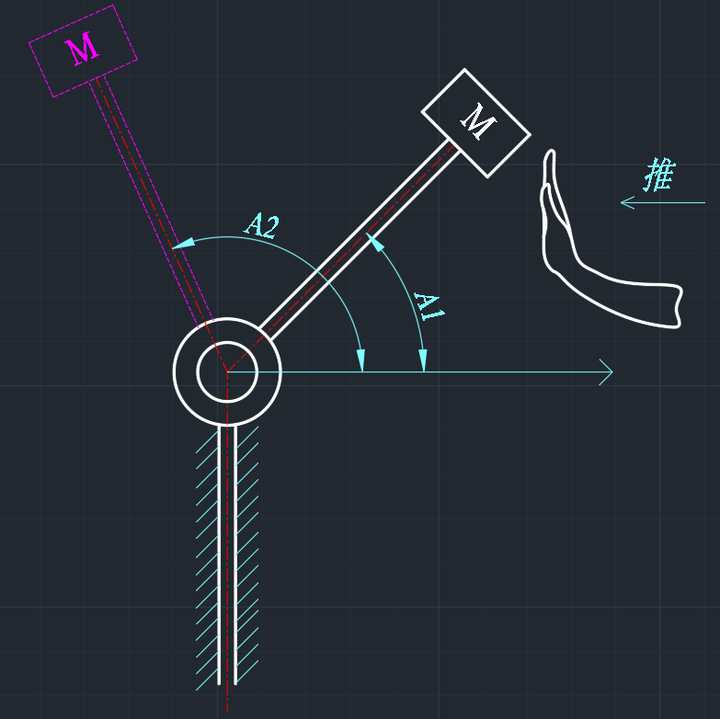
因为很灵敏,我推这个连上重物后的机械臂,与我直接推机械臂,相差的感觉就多了这个重物 带来的惯量,我得额外去克服这个惯量。就像,这个机械臂是水平放置的,水平面是冰面,我推这个重物机械臂很轻松,因为重物重量都被冰面承受了,但是我得额外克服因为重物带来的额外冰面摩擦力。尽管冰面很滑,这个摩擦力很小,但是摩擦力大小毕竟和重物重量正相关的。
假设冰面摩擦系数为0.1,那么我就得克服 的摩擦力。原本需要
大小的力去推这个重物到指定位置,现在只需要
的力去推它了,通过摩擦系数将操作力减小了0.1倍。在这里,灵敏度放大控制系统就像这个冰面,它承担了主要的负载,但是将移动负载的力缩小了,相应的,就是这个系统更加灵敏了。
但是要注意的是,我推了它,也要去“抓住”它,否则它就会在正反馈扰动下越转越快,直到不可控制。因此“冰面理论”并不是一个完全正确的理解思路,它只是能帮助理解在负重下的人机交互力。
更进一步
由上所述,图8的控制框图并不能完全反映BLEEX外骨骼和人的关系。因为穿戴者和外骨骼在足底上是绑定的,甚至为了穿戴稳定性,也可以在大腿或小腿处让外骨骼和人体绑定。所以人体和外骨骼其实是有运动上的联系的,需要在控制模型中反映这部分运动联系,因为它关系着人体对外骨骼造成的力矩 。
反过来想想,假如人与外骨骼没有这部分运动学联系,那人应该想怎么动就怎么动,为什么会被外骨骼的运动限制呢?理论上我劈个叉,外骨骼也会不管我而继续地走着,但这不可能。而且,如果穿戴者没有限制住外骨骼运动,就像上述的“抓不住”单关节机械臂一样,一下子就能导致失控。
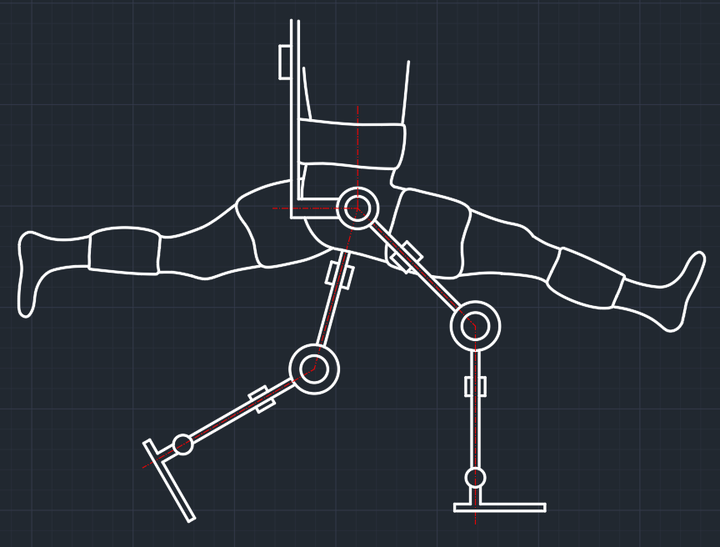
同时,BLEEX的团队认为,去建立一个穿戴者下肢整体模型是没有必要的,因为这其中包含的东西太多太复杂了,总不能去考虑人体神经信号的传输、肌肉的收缩、中枢神经的响应等这些过于细节的人体内部模型吧。
但是可以确定,穿戴者的动力学模型肯定不是线性的这么简单,那么可以定义一个非线性函数来反映穿戴者的下肢运动学。穿戴者与外骨骼有运动学关联部分的运动学参数在输进这个函数后,就会得到人体对外骨骼作用产生的力矩d。
毕竟外骨骼对穿戴者的运动造成了影响,穿戴者一定程度上受到了外骨骼带来的“阻力与抵抗”,因此BLEEX的团队将这种特性归为了阻抗特性。仔细理解这个特性我们发现,这种“抵抗”你、“逆”着你的行为,难道不是负反馈的意思么?比如,穿戴者的腿想要增加关节角度,而外骨骼阻碍了他,那么应该是向减少关节角度的趋势去阻碍。因此,这个非线性函数一定是负的。
考虑了以上关键因素后,定义外骨骼对人体运动学约束反馈的函数为H,习惯上将传递函数定义为正的,那么这个反馈函数H要加上负号才能体现上述所说的负反馈。实际的控制框图应该如下图所示。

框图里为负的函数比较反直觉,因为 和
都是相乘的关系,乘积结果前面也应该带有负号,何不将这个
号代替后续结点前的
号呢?因此,再次修改控制框图。
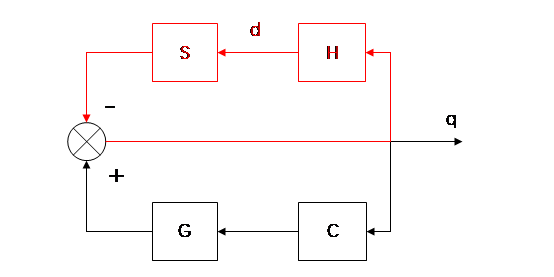
那么,图11就为BLEEX的灵敏度放大控制框图的终极版了(当然是经过细节简化后的)。可以看出该控制模型有两个环,上环是针对穿戴者的负反馈控制闭环,下环则由刚才前面所分析的,是外骨骼系统正反馈控制闭环。
灵敏度放大法的结论未变,当控制器 设计为
时,系统依然能够获得灵敏度放大的效果。图11只是比图8额外反映了外骨骼与人在运动学上的联系,这个控制框图代表的系统仍然是稳定的。但是要从理论上证明它是稳定的,需要进一步的探讨。
不过到目前为止,灵敏度放大法控制,GET!
为了从理论上证明图11是稳定的,并且试图看懂图11。
我们再次列些输出运动学的量q的表达式:
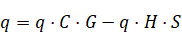
化简得:
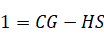
完蛋!好像更加不理解了!

为了解释以上的控制方程,我们需要使用小增益原理来阐释。但是这个有点超纲了,我们将在下一期专门用来讲解这个问题。这期就先打住吧。
挖坑!
参考文献:
[1] Kazerooni H, Racine J L, Huang L, et al. On the control of the berkeley lower extremity exoskeleton (BLEEX)[C]//Proceedings of the 2005 IEEE international conference on robotics and automation. IEEE, 2005: 4353-4360.
控制框图来自手打,表情包等图片来自网络
甲说,Logo升级!
该微信公众号和知乎专栏同步更新,几乎。
彩 蛋
由于在网络上关于小增益定理的科普或者讨论少之又少,我只好去知网查找小增益定理的论文学习学习,然后出现了下面的画面:



然后我就???

彩蛋完
https://zhuanlan.zhihu.com/p/109137487

